Vídeo: Por que os vetores são usados no aprendizado de máquina?
2024 Autor: Miles Stephen | [email protected]. Última modificação: 2023-12-15 23:39
No aprendizado de máquina , recurso vetores são usados para representar características numéricas ou simbólicas, chamadas de características, de um objeto de uma forma matemática e facilmente analisável. Elas são importantes para muitas áreas diferentes de aprendizado de máquina e processamento de padrões.
Então, o que é um vetor no aprendizado de máquina?
Vetor seja em Aprendizado de Máquina ou Álgebra Linear se refere ao mesmo - uma coleção / matriz de números - exemplo: [1, 3, 2] é um vetor . No aprendizado de máquina isto vetor é chamado de recurso vetor como cada um desses valores corresponde a algumas características, digamos, características de uma fruta em um problema de classificação de frutas.
Além disso, por que a Álgebra Linear é importante para o aprendizado de máquina? Matriz a fatoração é uma ferramenta chave em álgebra Linear e amplamente utilizado como um elemento de muitas operações mais complexas em ambos álgebra Linear (tais como o matriz inverso) e aprendizado de máquina (mínimos quadrados). Para ler e interpretar de ordem superior matriz operações, você deve entender matriz fatoração.
Também para saber, o que é um vetor em ML?
Por que as matrizes com dimensões Nx1 são chamadas vetores Se você estudou física ou engenharia em nível universitário, provavelmente pensa em vetores como algo que tem magnitude e direção onde o comprimento do vetor é a magnitude e a orientação do vetor é a direção.
O que é recurso no aprendizado de máquina?
No aprendizado de máquina e reconhecimento de padrões, um recurso é uma propriedade individual mensurável ou característica de um fenômeno sendo observado. O conceito de" recurso "está relacionada à variável explicativa utilizada em técnicas estatísticas, como a regressão linear.
Recomendado:
Por que é correto dizer que a energia é conservada em uma máquina?
Por que é correto dizer que a ENERGIA É CONSERVADA em uma máquina? A energia é conservada localmente (ou seja, pode se mover, mas não pode pular) em todos os lugares do universo. Sua máquina pode "desperdiçar" energia transformando parte dela em calor, mas você não pode realmente destruir ou criar energia
O que é passeio aleatório no aprendizado de máquina?
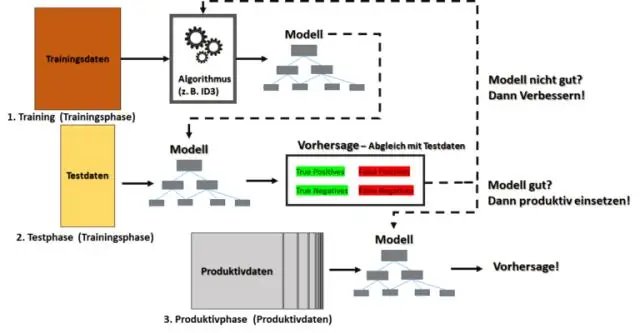
R: No aprendizado de máquina, uma abordagem de 'passeio aleatório' pode ser aplicada de várias maneiras para ajudar a tecnologia a filtrar os grandes conjuntos de dados de treinamento que fornecem a base para a compreensão final da máquina. Um passeio aleatório, matematicamente, é algo que pode ser descrito de várias maneiras técnicas diferentes
Por que espelhos convexos são usados em supermercados?
O espelho convexo é usado nos supermercados porque cobre uma ampla área nas câmeras cc e torna os vegetais e frutas visíveis adequadamente
O que são vetores padrão?
Os vetores unitários padrão. Um vetor unitário é um vetor cuja magnitude (ou comprimento) é um. Os vetores unitários padrão são os vetores unitários especiais que são paralelos aos eixos das coordenadas, apontando para os valores positivos da coordenada
O que são vetores no pré-cálculo?
Definição de vetor. Um vetor é um objeto que possui magnitude e direção. Geometricamente, podemos imaginar um vetor como um segmento de linha direcionado, cujo comprimento é a magnitude do vetor e com uma seta indicando a direção. Dois exemplos de vetores são aqueles que representam força e velocidade