
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Última modificação 2025-01-22 17:07.
Domínio restrições de um função racional pode ser determinado definindo o denominador igual a zero e resolvendo. Os valores de x em que o denominador é igual a zero estão chamadas de singularidades e estão não está no domínio do função.
Da mesma forma, por que as funções racionais são importantes?
Significado. " Função racional "é o nome dado a um função que pode ser representado como o quociente de polinômios, assim como um racional number é um número que pode ser expresso como um quociente de números inteiros. Funções racionais fornecem importante exemplos e ocorrem naturalmente em muitos contextos.
Da mesma forma, as funções racionais têm pontos de inflexão? 4Resumo. Um polinômio de grau n tem no máximo n zeros reais en − 1 pontos de viragem . UMA função racional é um função da forma f (x) = P (x) Q (x), f (x) = P (x) Q (x), onde P (x) e Q (x) estão ambos os polinômios.
Também a questão é: o que é um exemplo de função racional?
Exemplos do Funções Racionais o função R (x) = (x ^ 2 + 4x - 1) / (3x ^ 2 - 9x + 2) é um função racional uma vez que o numerador, x ^ 2 + 4x - 1, é um polinômio e o denominador, 3x ^ 2 - 9x + 2 também é um polinômio.
Quais são as características das funções racionais?
Dois importantes recursos de qualquer função racional r (x) = p (x) q (x) r (x) = p (x) q (x) são quaisquer zeros e assíntotas verticais os função pode ter. Esses aspectos de um função racional estão intimamente ligados a onde o numerador e denominador, respectivamente, são zero.
Recomendado:
Por que declaramos restrições para a expressão racional e quando declaramos as restrições?

Declaramos restrições porque pode fazer com que a equação seja indefinida em alguns valores de x. A restrição mais comum para expressões racionais é N / 0. Isso significa que qualquer número dividido por zero é indefinido. Por exemplo, para a função f (x) = 6 / x², quando você substitui x = 0, resultaria em 6/0, que é indefinido
Como aplico restrições dimensionais no AutoCAD?
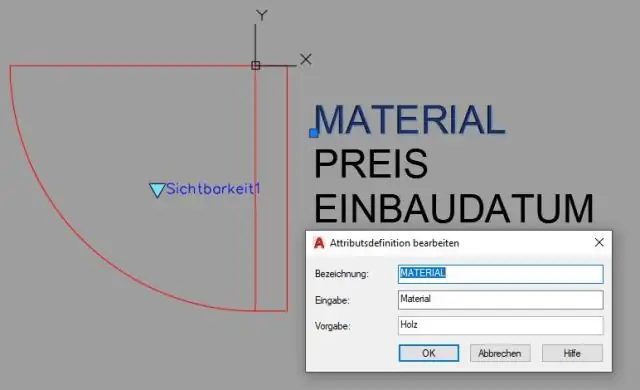
Estas etapas apresentam um exemplo simples de restrições dimensionais: Inicie um novo desenho e torne a guia Paramétrica da Faixa de opções atual. Ative os auxílios de desenho de precisão apropriados na barra de status, como Snap, Ortho e Osnap. Desenhe alguma geometria razoavelmente precisa, aplicando uma técnica de precisão
Por que as funções trigonométricas são chamadas de funções circulares?

As funções trigonométricas às vezes são chamadas de funções circulares. Isso ocorre porque as duas funções trigonométricas fundamentais - o seno e o cosseno - são definidas como as coordenadas de um ponto P viajando no círculo unitário de raio 1. O seno e o cosseno repetem suas saídas em intervalos regulares
Como você encontra as restrições de uma expressão racional?

A restrição é que o denominador não pode ser igual a zero. Portanto, neste problema, como 4x está no denominador, não pode ser igual a zero. Encontre todos os valores de x que fornecem um zero no denominador. Para encontrar as restrições em uma função racional, encontre os valores da variável que tornam o denominador igual a 0
Como você multiplica funções racionais?

Q e S não são iguais a 0. Etapa 1: Fatore o numerador e o denominador. Etapa 2: escreva como uma fração. Etapa 3: Simplifique a expressão racional. Etapa 4: multiplique todos os fatores restantes no numerador e / ou denominador. Etapa 1: fatorar o numerador e o denominador. Etapa 2: escreva como uma fração
