Índice:
Vídeo: Como você resolve um problema de programação linear pelo método dos cantos?
2024 Autor: Miles Stephen | [email protected]. Última modificação: 2023-12-15 23:39
A MÉTODO DE CANTOS Represente graficamente o conjunto viável (região), S. Encontre o Coordenadas EXATAS de todos os vértices ( canto pontos) de S. Avalie a função objetivo, P, em cada vértice O máximo (se existir) é o maior valor de P em um vértice. O mínimo é o menor valor de P em um vértice.
Posteriormente, também se pode perguntar: quais são os métodos para resolver LPP?
Método gráfico de resolução de problemas de programação linear
- Vídeos sugeridos.
- Etapa 1: Formule o problema LP (programação linear).
- Etapa 2: Construa um gráfico e plote as linhas de restrição.
- Etapa 3: Determine o lado válido de cada linha de restrição.
- Etapa 4: identificar a região de solução viável.
- Etapa 5: trace a função objetivo no gráfico.
- Etapa 6: Encontre o ponto ideal.
o que é método algébrico em programação linear? Álgebra e o Simplex Método . UMA problema de programação linear (LP) é um problema de otimização onde todas as variáveis são contínuas, o objetivo é um linear (no que diz respeito às variáveis de decisão) função, e a região viável é definida por um número finito de linear desigualdades ou equações.
Aqui, como você calcula os pontos de canto na programação linear?
o pontos de canto são os vértices da região viável. Depois de ter o gráfico do sistema de linear desigualdades, então você pode olhar para o gráfico e facilmente dizer onde o pontos de canto estão. Você pode precisar resolver um sistema de linear equações para achar algumas das coordenadas do pontos no meio.
Qual é o método de solução de ponto de canto?
o método de solução de ponto de canto consiste em quatro etapas principais:: Determinar as coordenadas de cada vértice ( ponto de canto ) da região viável.: Calcule o valor da função objetivo em cada ponto de canto .: Estabeleça a função objetivo com o valor máximo.
Recomendado:
Como você resolve um problema de proporção?
Primeiro, escreva a proporção, usando uma letra para representar o termo ausente. Encontramos os produtos cruzados multiplicando 20 vezes x e 50 vezes 30. Em seguida, divida para encontrar x. Estude esta etapa com atenção, porque esta é uma técnica que usaremos com frequência em álgebra
Como você resolve um problema de inclinação?
Identifique a inclinação, m. Isso pode ser feito calculando a inclinação entre dois pontos conhecidos da linha usando a fórmula da inclinação. Encontre a interceptação y. Isso pode ser feito substituindo a inclinação e as coordenadas de um ponto (x, y) na linha na fórmula inclinação-interceptação e, em seguida, resolva para b
Como você resolve equações lineares pelo método gráfico?
Uma solução gráfica pode ser feita manualmente (em papel milimetrado) ou com o uso de uma calculadora gráfica. Representar graficamente um sistema de equações lineares é tão simples quanto representar graficamente duas linhas retas. Quando as linhas são representadas graficamente, a solução será o par ordenado (x, y) onde as duas linhas se cruzam (cruzam)
Como você resolve um problema de circuito em série?
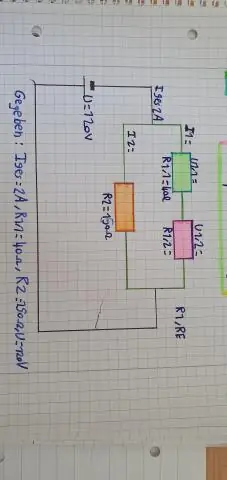
VÍDEO Então, o que é um exemplo de circuito em série? Um exemplo de um circuito em série é uma série de luzes de Natal. Se alguma das lâmpadas estiver faltando ou queimada, nenhuma corrente fluirá e nenhuma das luzes se acenderá. Paralelo circuitos são como os vasos sanguíneos menores que se ramificam de uma artéria e se conectam a uma veia para retornar o sangue ao coração.
Qual é o método simplex para programação linear?
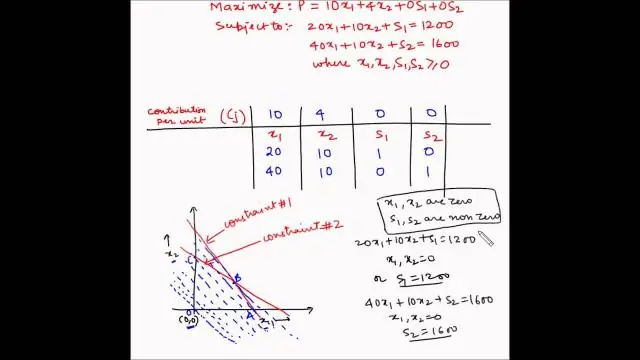
Método simplex. Método Simplex, técnica padrão em programação linear para resolver um problema de otimização, normalmente envolvendo uma função e várias restrições expressas como desigualdades. As desigualdades definem uma região poligonal (veja o polígono), e a solução está normalmente em um dos vértices