Índice:
Vídeo: O que é relação em álgebra?
2024 Autor: Miles Stephen | [email protected]. Última modificação: 2023-12-15 23:39
UMA relação é um relação entre conjuntos de valores. Em matemática, o relação está entre os valores xey dos pares ordenados. O conjunto de todos os valores x é chamado de domínio e o conjunto de todos os valores y é chamado de intervalo. Os colchetes são usados para mostrar que os valores formam um conjunto.
Simplesmente assim, qual é a definição de relação em matemática?
Definição de relação . UMA relação entre dois conjuntos está uma coleção de pares ordenados contendo um objeto de cada conjunto. Se o objeto x é do primeiro conjunto e o objeto y é do segundo conjunto, então os objetos são considerados relacionados se o par ordenado (x, y) estiver no relação . Uma função é um tipo de relação.
Também se pode perguntar: qual é a função na álgebra? UMA função é uma equação que tem apenas uma resposta para y para cada x. UMA função atribui exatamente uma saída para cada entrada de um tipo especificado. É comum nomear um função ou f (x) ou g (x) em vez de y. f (2) significa que devemos encontrar o valor de nossa função quando x é igual a 2.
Posteriormente, a questão é: qual é a diferença entre uma relação e uma função na álgebra?
Resumo da lição A relação é um conjunto de entradas e saídas relacionadas de alguma forma. Quando cada entrada em uma relação tem exatamente uma saída, o relação é dito ser um função . Para determinar se um relação é um função , garantimos que nenhuma entrada tenha mais de uma saída.
Quais são os 3 tipos de relação em matemática?
Existem diferentes tipos de relações, nomeadamente reflexivas, simétricas, transitivas e anti-simétricas, que são definidas e explicadas a seguir através de exemplos da vida real
- Relação reflexiva: diz-se que uma relação R é reflexiva sobre um conjunto A se (a, a) € R para cada a € R.
- Relação simétrica:
- Relação transitiva:
Recomendado:
O que é uma relação interespecífica?
Existem diversos organismos que estão presentes na comunidade e por isso; relacionamentos diferentes são desenvolvidos entre eles. As relações interespecíficas são as relações que mostram as interações entre os organismos pertencentes a diferentes espécies
Qual é a diferença entre Álgebra 1 e Álgebra 2?
O foco principal da Álgebra 1 é resolver equações. As únicas funções que você examinará extensivamente são lineares e quadráticas. Álgebra 2 é muito mais avançado
Qual é o nome que se dá a uma relação simbiótica em que ambas as espécies se beneficiam?
Mutualismo é uma relação simbiótica em que ambas as espécies se beneficiam. Comensalismo é uma relação simbiótica em que uma espécie se beneficia enquanto a outra espécie não é afetada. O parasitismo é uma relação simbiótica na qual uma espécie (o parasita) se beneficia enquanto a outra espécie (o hospedeiro) é prejudicada
O que acontece durante a interfase em relação ao DNA que é importante para a divisão celular?
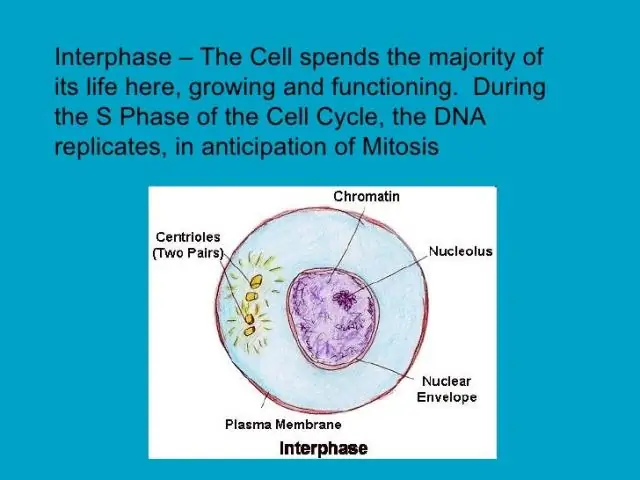
Durante a interfase, uma célula aumenta de tamanho, sintetiza novas proteínas e organelas, replica seus cromossomos e se prepara para a divisão celular, produzindo proteínas do fuso. Antes da divisão celular, os cromossomos são replicados, de modo que cada cromossomo consiste em duas cromátides "irmãs" idênticas
Álgebra intermediária é Álgebra 2?
Este livro didático de Álgebra Intermediária foi elaborado como um curso cronológico para guiá-lo através da Álgebra do Ensino Médio (às vezes chamada de Álgebra II em alguns locais). Este livro supõe que você tenha concluído Aritmética e Álgebra. Embora não seja obrigatório, a Álgebra Intermediária normalmente é tirada um ano após a Geometria