
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Última modificação 2025-01-22 17:08.
o função de distribuição radial dá o densidade de probabilidade para um elétron ser encontrado em qualquer lugar na superfície de uma esfera localizada a uma distância r do próton. Uma vez que a área de uma superfície esférica é 4πr2, o função de distribuição radial é dado por (4 pi r ^ 2 R (r) ^ * R (r)].
Então, o que é densidade de probabilidade radial?
Densidade de probabilidade em um determinado ponto significa probabilidade por volume no limite em que o volume é infinitesimalmente pequeno. Distribuição de probabilidade radial em um determinado raio é o probabilidade por distância que o evento ocorre em uma casca esférica infinitesimalmente fina naquele raio.
Da mesma forma, o que é uma função de onda radial? Aceno equação, ψ Um orbital é um matemático função chamado de função de onda que descreve um elétron em um átomo. Funções de onda radial pois um dado átomo depende apenas da distância, r, do núcleo. Angular funções de onda dependem apenas da direção e, de fato, descrevem a forma de um orbital.
Correspondentemente, qual é a curva de distribuição de probabilidade radial?
Curva de distribuição radial dá uma ideia sobre o elétron densidade em um radial distância do núcleo. O valor de 4πr2ψ2 ( função de densidade de probabilidade radial ) torna-se zero em um ponto nodal, também conhecido como um radial nó. O número de radial nós para um orbital = n-l-1.
Qual é a diferença entre a densidade de probabilidade em função de R e a função de probabilidade radial em função de R?
(UMA) Densidade de probabilidade em função de r é probabilidade de encontrar o elétron em um ponto específico no espaço à distância ' r 'do núcleo, enquanto o função de probabilidade radial de 'r 'é P ( r ) é o probabilidade de encontrar elétrons em qualquer ponto à distância ' r 'do núcleo.
Recomendado:
O que acontece quando a densidade fisiológica é maior do que a densidade aritmética?
A densidade fisiológica ou densidade populacional real é o número de pessoas por unidade de área de arableland. Uma densidade fisiológica mais alta sugere que a terra agrícola disponível está sendo usada por mais pessoas e pode atingir seu limite de produção mais cedo do que um país com densidade fisiológica mais baixa
Qual é a curva de distribuição de probabilidade radial?

A curva de distribuição radial dá uma ideia sobre a densidade de elétrons a uma distância radial do núcleo. O valor de 4 π r2ψ2 (função de densidade de probabilidade radial) torna-se zero em um ponto nodal, também conhecido como nó radial. Onde n = número quântico principal e l = número quântico azimutal
O que é densidade no gráfico de densidade?

Um gráfico de densidade é uma representação da distribuição de uma variável numérica. Ele usa uma estimativa de densidade de kernel para mostrar a função de densidade de probabilidade da variável (veja mais). É uma versão suavizada do histograma e é usado no mesmo conceito
Qual é a diferença entre fatores independentes de densidade e fatores dependentes de densidade com exemplos?

Opera em populações grandes e pequenas e não se baseia na densidade populacional. Os fatores dependentes da densidade são aqueles que regulam o crescimento de uma população dependendo de sua densidade, enquanto os fatores independentes da densidade são aqueles que regulam o crescimento populacional sem depender de sua densidade
Qual é a diferença entre probabilidade condicional e probabilidade conjunta?
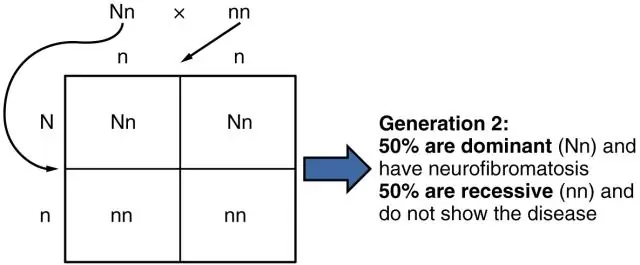
Em termos gerais, a probabilidade conjunta é a probabilidade de duas coisas * acontecerem juntas: por exemplo, a probabilidade de eu lavar meu carro e chover. A probabilidade condicional é a probabilidade de uma coisa acontecer, dado que a outra acontece: por exemplo, a probabilidade de que, dado que eu lavo meu carro, chove
