Vídeo: Como você encontra o centro de um círculo em uma seção cônica?
2024 Autor: Miles Stephen | [email protected]. Última modificação: 2023-12-15 23:39
O valor de r é chamado de "raio" do círculo , e o ponto (h, k) é chamado de " Centro "do círculo . (h, k) = (0, 0), então a equação simplifica o x2 + y2 = r2.
Levando isso em consideração, como você resolve uma seção cônica de um círculo?
Seção Cônica do Círculo Ao trabalhar com seções cônicas do círculo , podemos ver a equação de um círculo usando as coordenadas e a fórmula de distância. A equação de um círculo é (x -h)2 + (y - k)2 = r2 onde r é igual ao raio e as coordenadas (x, y) são iguais ao círculo Centro.
como você encontra o ponto central de um círculo? o Centro - forma de raio do círculo a equação está no formato (x - h)2 + (y –k)2 = r2, com o Centro estar no apontar (h, k) e o raio sendo "r". Esta forma da equação é útil, pois você pode facilmente achar a Centro e o raio.
Da mesma forma, as pessoas perguntam: qual é a seção cônica de um círculo?
Como um seção cônica , a círculo é a intersecção de um plano perpendicular ao eixo do cone. A definição geométrica de um círculo é o lugar geométrico de todos os pontos a uma distância constante r {estilo de exibição r} de um ponto (h, k) {estilo de exibição (h, k)} e formando a circunferência (C).
O que é um círculo em álgebra?
UMA círculo é definido como o conjunto de pontos cuja distância fixa é de um ponto central. Esta definição é expressa na forma como desenhamos círculos . Escolhemos um ponto como o centro e, em seguida, usamos alguns meios mecânicos para girar um utensílio de desenho ao redor desse ponto.
Recomendado:
Como você faz uma seção fina?
Este processo é simples: certifique-se de que a seção esteja limpa e sem grãos ou sujeira. Coloque-o na chapa quente. Misture um pequeno lote de epóxi e endurecedor. Coloque uma pequena gota de epóxi no corte. Solte uma lamínula na queda. Mova-o para expelir as bolhas e cubra totalmente a seção. Deixe curar
Como você encontra a seção transversal de um quadrado?
VÍDEO Tendo isso em vista, qual é a seção transversal de um quadrado? Cruzamentos . UMA corte transversal é a forma que obtemos quando cortamos um objeto direto. o corte transversal deste objeto é um triângulo. É como uma visão do interior de algo feito ao cortá-lo.
Como você renomeia uma tag de seção no Revit?
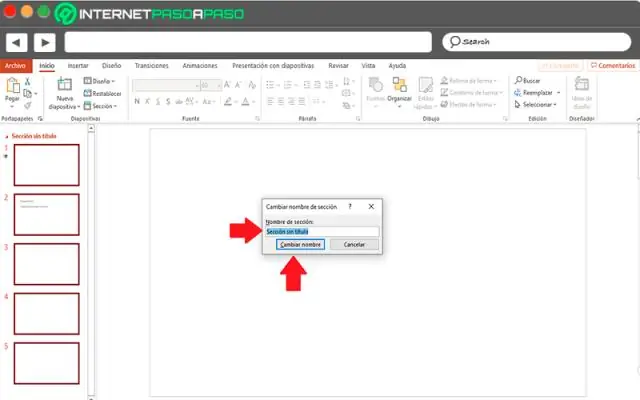
Clique na guia Gerenciar painel Configurações menu suspenso Configurações adicionais (Tags de seção). Na caixa de diálogo Propriedades de tipo, clique em Duplicar. Insira um nome para o novo cabeçalho de seção e clique em OK
Como você representa o gráfico de uma cônica de uma parábola?
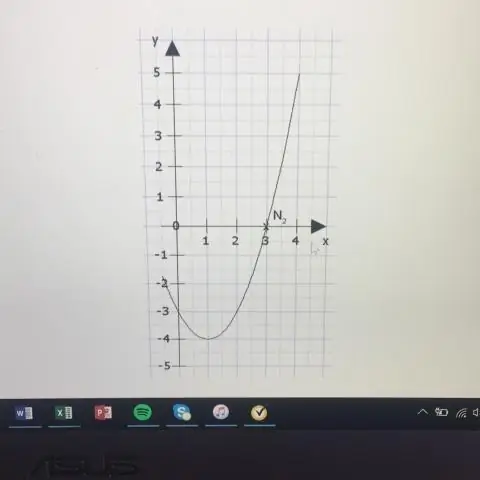
A diretriz é a linha y = k - p. O eixo é a linha x = h. Se p> 0, a parábola abre para cima, e se p <0, a parábola abre para baixo. Se uma parábola tem um eixo horizontal, a forma padrão da equação da parábola é esta: (y - k) 2 = 4p (x - h), onde p ≠ 0
Como você faz uma seção cônica de uma parábola?
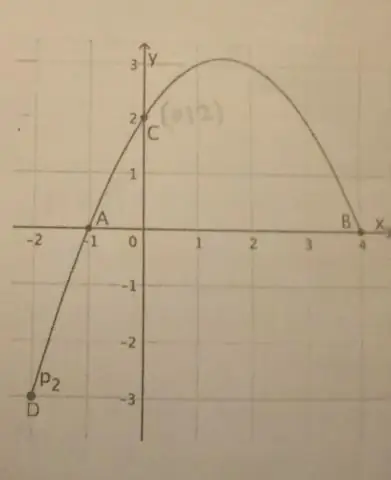
Se uma parábola tem um eixo vertical, a forma padrão da equação da parábola é esta: (x - h) 2 = 4p (y - k), onde p ≠ 0. O vértice desta parábola está em (h, k). O foco está em (h, k + p). A diretriz é a linha y = k - p