- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Última modificação 2025-01-22 17:07.
Avaliação de funções compostas usando gráficos
- Localize a entrada fornecida para o interior função no eixo x de seu gráfico.
- Leia a saída do interior função do eixo y de seu gráfico.
- Localize o interior função saída no eixo x do gráfico do exterior função .
Aqui, como você escreve e avalia funções compostas?
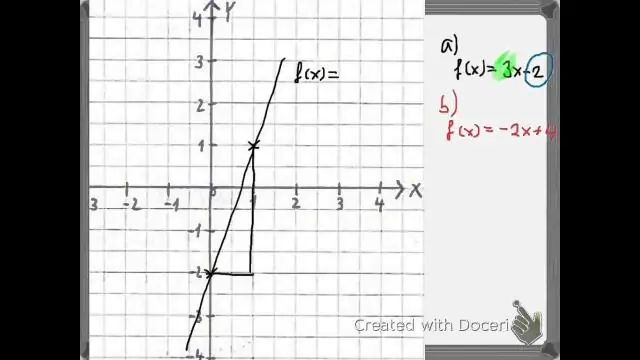
Fazer um função composta onde colocamos g (x) dentro do função f (x), podemos escrever it f (g (x)). Observe que em vez de simplesmente colocar um x no função , substituímos todo o g (x) função . Quando fazemos isso, temos f (g (x)) = (3x) + 2. À esquerda, você verá que o g função está dentro do f função.
Da mesma forma, o que é um exemplo de função composta? UMA função composta é um função isso depende de outro função . UMA função composta é criado quando um função é substituído por outro função . Para exemplo , f (g (x)) é o função composta que é formado quando g (x) é substituído por x em f (x). No composição (f ο g) (x), o domínio de f torna-se g (x).
As pessoas também perguntam quais são as etapas para resolver uma função composta?
Aqui está o degraus podemos usar para encontrar o composição de dois funções : Etapa 1: Reescreva o composição em uma forma diferente. Por exemplo, o composição (f g) (x) precisa ser reescrito como f (g (x)). Etapa 2: Substitua cada ocorrência de x encontrada na parte externa função com o interior função.
O que se entende por função composta?
: uma função cujos valores são encontrados a partir de dois dados funções aplicando um função a uma variável independente e, em seguida, aplicando o segundo função ao resultado e cujo domínio consiste naqueles valores da variável independente para o qual o resultado gerado pelo primeiro função encontra-se no domínio do segundo.
Recomendado:
Como você multiplica funções compostas?

Multiplicação e composição de funções Para multiplicar uma função por um escalar, multiplique cada saída por esse escalar. Quando tomamos f (g (x)), tomamos g (x) como a entrada da função f. Por exemplo, se f (x) = 10x e g (x) = x + 1, então para encontrar f (g (4)), encontramos g (4) = 4 + 1 + 5, e então avaliamos f (5 ) = 10 (5) = 50. Exemplo: f (x) = 2x - 2, g (x) = x2 - 8
Como você encontra as funções trigonométricas do arco?

Denotamos a função inversa como y = sin &menos; 1 (x). É lido que y é o inverso de seno x e significa que y é o ângulo de número real cujo valor de seno é x. Tenha cuidado com a notação usada. Gráficos de funções trigonométricas inversas. Intervalo de domínio de função csc − 1 (x) (− ∞, − 1] ∪ [1, ∞) [− π 2,0) ∪ (0, π 2]
Por que as funções trigonométricas são chamadas de funções circulares?

As funções trigonométricas às vezes são chamadas de funções circulares. Isso ocorre porque as duas funções trigonométricas fundamentais - o seno e o cosseno - são definidas como as coordenadas de um ponto P viajando no círculo unitário de raio 1. O seno e o cosseno repetem suas saídas em intervalos regulares
Como você representa graficamente as funções logarítmicas em uma calculadora?

Na calculadora gráfica, o logaritmo de base e é a tecla ln. Todos os três são iguais. Se você tiver a função logBASE, ela pode ser usada para inserir a função (visto em Y1 abaixo). Caso contrário, use a fórmula de Mudança de Base (ver em Y2 abaixo)
Como você transforma funções lineares?
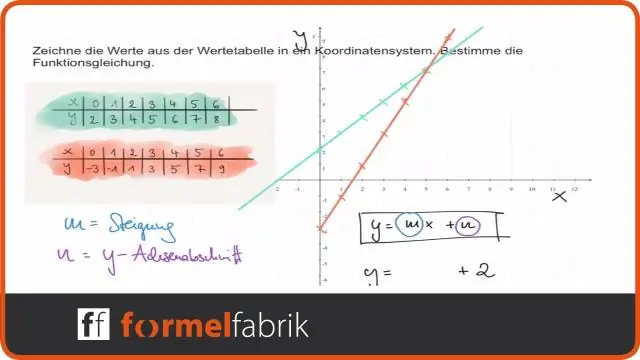
Como: Dada a equação de uma função linear, use transformações para representar graficamente a função linear na forma f (x) = mx + b f (x) = m x + b. Gráfico f (x) = x f (x) = x. Estique ou comprima verticalmente o gráfico por um fator | m |. Muda o gráfico para cima ou para baixo unidades b
